Valid Colors in the CIE 1976 Lab Color Space
August 23, 2011I was curious about which values are valid in the CIELAB color space. The lightness coordinate, L, is defined to range from 0 to 100, but the chromaticity coordinates, a and b, have no defined bounds. So I wrote a program to find which CIELAB coordinates can be created physically.
Each wavelength of light produces a well defined color that be found in a table. But as most colors are a combination of different wavelengths, you need to solve a number of equations to find which wavelengths that are needed to create that color. This can be modeled as a Linear Programming Problem. A color is physically possible if the Linear Programming Problem has at least one solution.
I ran the program to create images of the a and b plane for a given L-value. The Physically reproducible colors are drawn in a light gray color, and if the color is whithin the sRGB gamut, it is drawn as is.
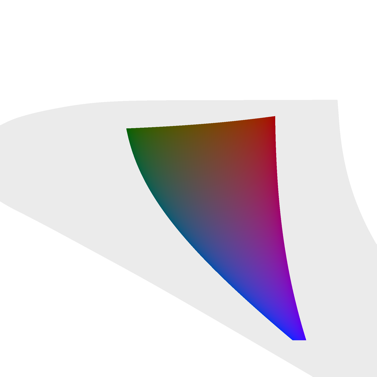 |
| L* = , a* ∈ [-128, 128], b* ∈ [-128, 128] |
References
- A Standard Default Color Space for the Internet - sRGB, M. Stokes, M. Anderson, S. Chandrasekar, R. Motta 1996. http://www.color.org/sRGB.xalter
- CIE 1931 color space, Wikipedia. http://en.wikipedia.org/wiki/CIE_1931_color_space
- Lab color space, Wikipedia. http://en.wikipedia.org/wiki/Lab_color_space
- Color Science, 2nd Edition, G. Wyszecki, W.S. Stiles 2000. ISBN 978-0-471-39918-6.
- Linear Programming, Wikipedia. http://en.wikipedia.org/wiki/Linear_programming